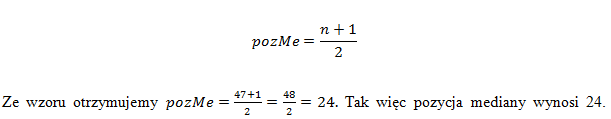Mediana

Mediana – Miara centralna w rozkładzie zmiennych. Określa wartość środkową rozkładu, dla której dokładnie połowa wyników jest mniejsza bądź równa od niej a druga połowa jest dokładnie większa bądź równa od niej. Można ją znaleźć szeregując wyniki od najmniejszego do największego i wyznaczając dokładnie liczbę środkową. W przypadku gdy jest parzysta liczba wyników to należy wyciągnąć średnią z 2 środkowych.

W nieco inny sposób oblicza się medianę, gdy mamy do czynienia z szeregiem rozdzielczym. Rozpatrzmy to na przykładzie:

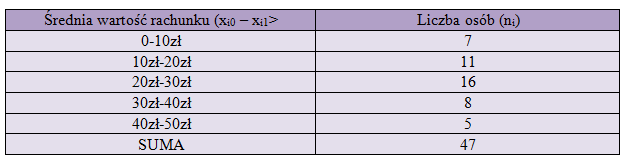
Przy osiedlowym małym sklepiku zapytano klientów z jakiego przedziału cenowego była wartość ich rachunku. Chcemy znaleźć wartość środkową ich rachunków. Na początek trzeba sprawdzić, w którym z przedziałów będzie znajdować się mediana. W tym celu stosujemy wzór:

Następnie obliczamy wartości skumulowane dla przedziałów, jak w tabelce poniżej.

Teraz należy sprawdzić, w której liczebność skumulowanej po raz pierwszy znajduje się wartość mediany czyli 24. Tak więc 24 nie zawiera się w 7, nie zawiera też się w 18, ale zawiera się już w 34. Trzeci przedział jest więc przedziałem, w którym znajduje się mediana. Teraz posługujemy się wzorem:

Można więc powiedzieć, że połowa klientów osiedlowego sklepu wydawała mniej niż 23,75zł, a druga połowa wydawała więcej od tej kwoty.